Abstract.
We present an experimental and theoretical study of the photonic band gap in the propagation of surface plasmons (SPs) on periodically corrugated surfaces. Our main purpose is to investigate the case where the band gap width is larger than the energy distance between the SP dispersion curve for a flat surface and the light line. We introduce a physical model of the interaction of light waves with SPs and derive an analytical expression for the SP wavevector near band gaps based on the coupled-mode approach involving three interacting modes (two of them are SP modes and one is a light mode). By using the interferometric measurement we have studied for the first time the SP propagation parameters in the vicinity of the photonic band gap (10 mkm wavelength region). The predictions of our theory are in good agreement with the experimental data.

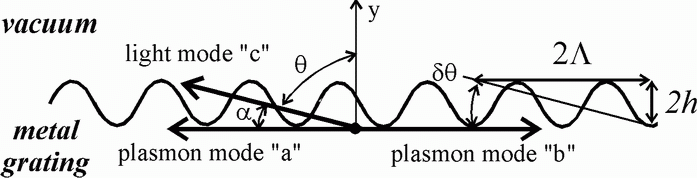
Fig.2 A schematic illustration of the interaction between scattered light wave "c" and plasmon wave "b" at the metal grating.

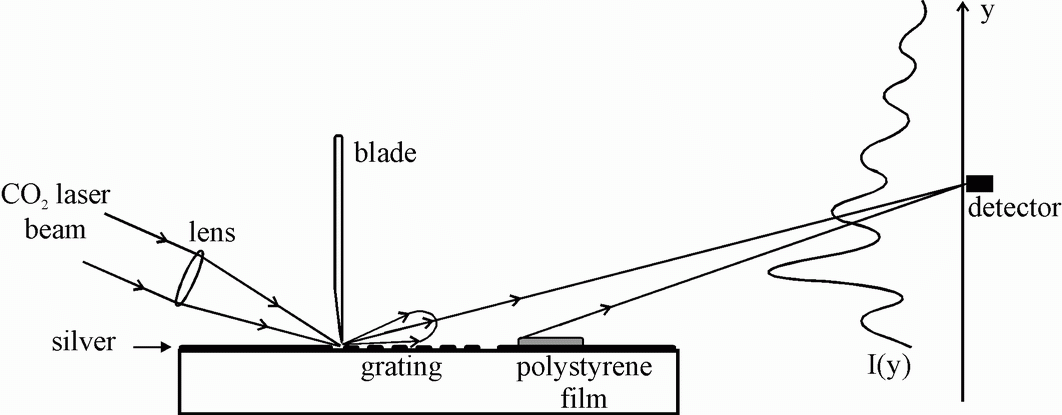
Fig.5 The optical scheme for measurements of SP propagation parameters.

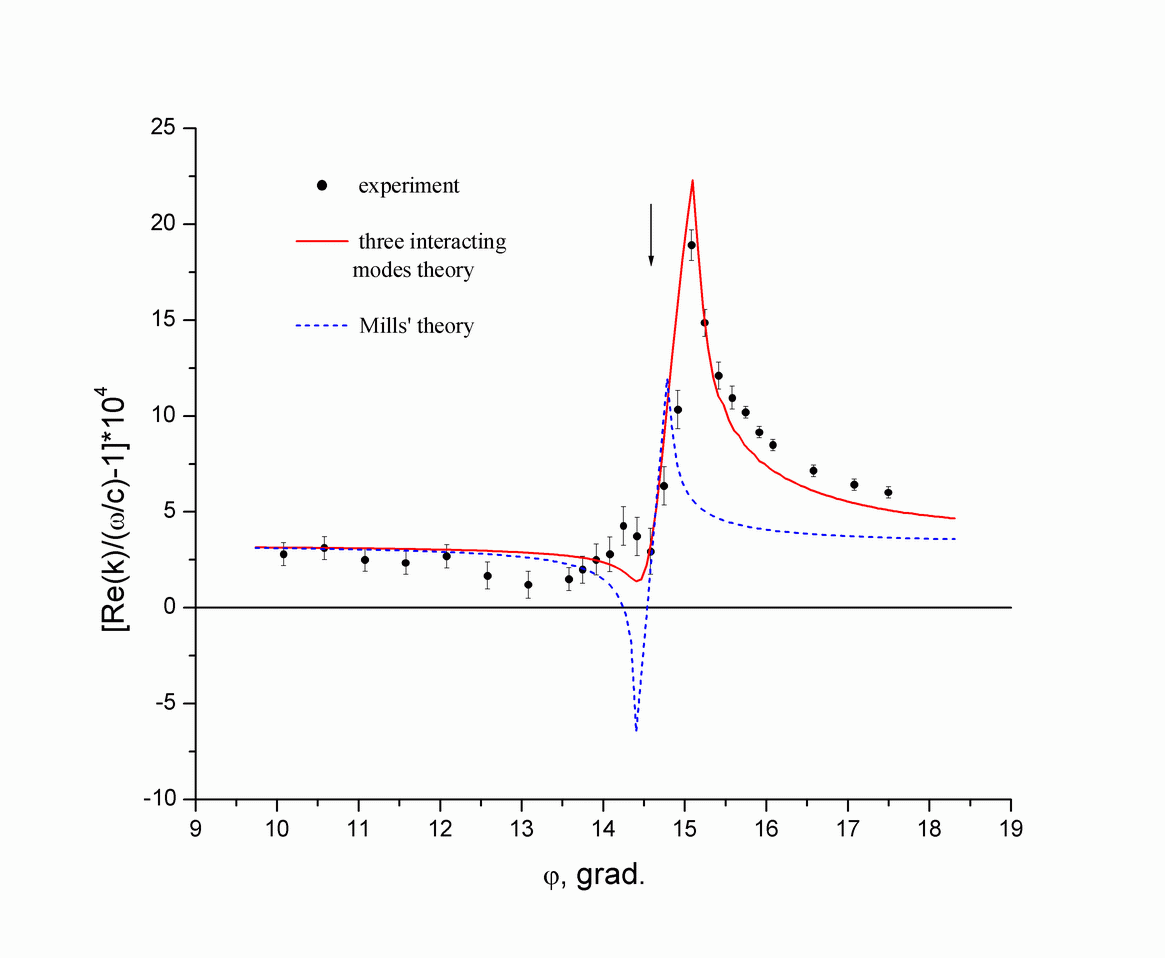
Fig.6 The real part of the SP wavevector on a silver grating as a function of the angle $\varphi$ between the SP propagation direction and the Bragg vector of the grating. The experimental values are represented by circles (the error bar indicates the accuracy of measurements). The dashed line corresponds to Mills' theory and the solid line --- to the coupled-mode approach with three interacting modes.

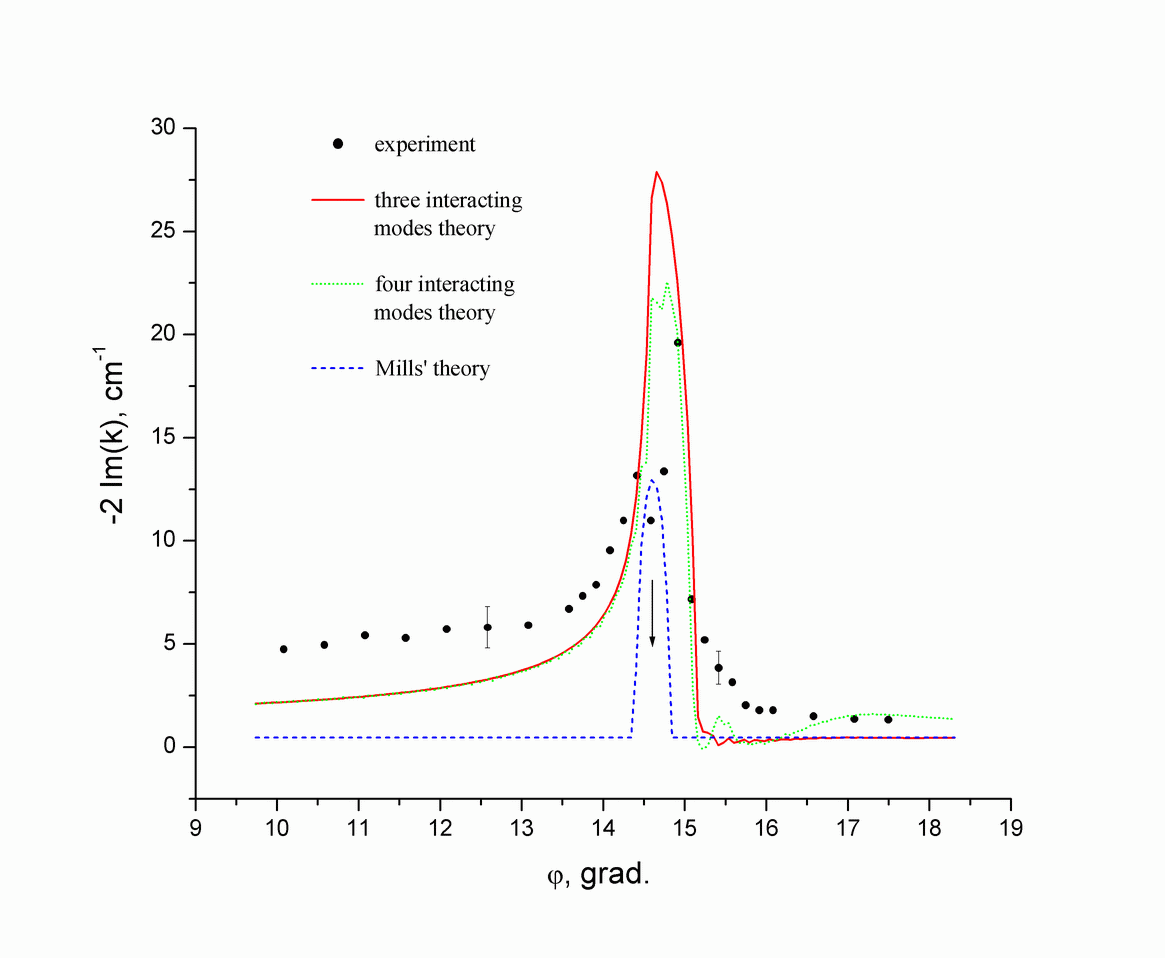
Fig.7 The imaginary part of the SP wavevector on silver grating as a function of the angle $\varphi$ between the SP propagation direction and the Bragg vector of the grating. The experimental values are represented by circles, the dashed line corresponds to Mills' theory, the solid line --- to the coupled-mode approach with three interacting modes and the dotted line --- to that with four interacting modes.

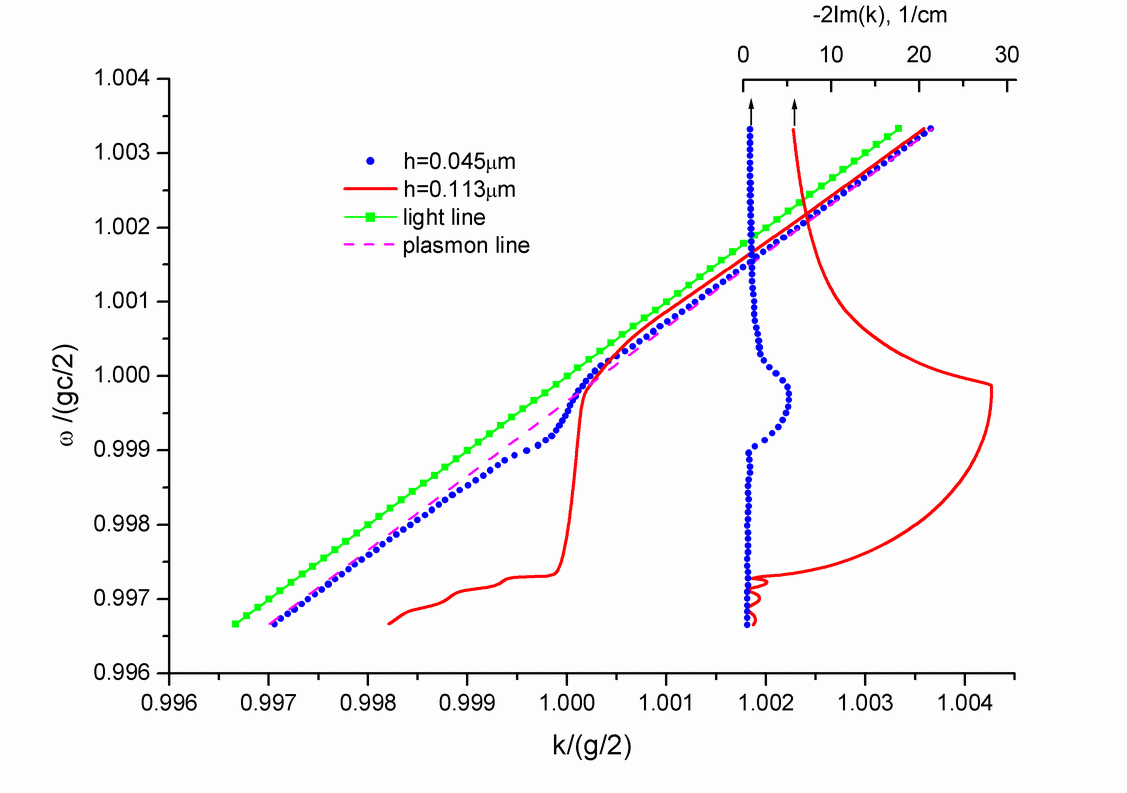
Fig.8 The theoretically calculated dispersion curves of SP on the grating at $\varphi=0$ with different corrugation amplitudes $h$ of the first Fourier component. The dashed line shows the SP dispersion curve for a flat metal surface, the dotted line that for h=0.045 mkm and the solid line that for h=0.113 mkm (it is the real amplitude of our grating).